Question

2. Solve the following system of equations.

f(x) = 2x^2 – 5x– 7
g(x) = -4x^2+16
O (-1.2,17.88) and (-1.5, 17)
O (2.42,-7.4) and (-1.58, 5.9)
(-1.5, 17) and (3.7, 1788)
O (2.4,- 44) and (3.7, 17.88)

Answer 1

Cited by 3 — —1.4 p F, ~ +~~• 3*,7 38 4.0 7 h m 0 16 44.20 17 25.10 —0.7 3326~7 ... O—1.2 —1.4 F ~ ,F~ ~ 7.8 38 26.6 m ~ .8 ~5 2~5 44;65 26 2.95 h -4

Step-by-step explanation:i know

Answer 2

(2.42,-7.4) and (-1.58, 5.9)

Step-by-step explanation:

• f(x) = 2x² – 5x– 7

• g(x) = -4x² + 16

Solve algebraically:

⇒ f(x) = g(x)

⇒ 2x² – 5x– 7 = -4x² + 16

⇒ 2x² - 5x - 7 + 4x² - 16 = 0

⇒ 6x² -5x -23 = 0

Now use the quadratic function:
`\boxed{ \sf x = (-b\pm√(b^2 - 4ac) )/(2a)}`

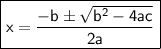
Identify : a = 6, b = -5, c = -23

Solving Step Wise:

`\rightarrow \sf x = (-(-5)\pm√((-5)^2 - 4(6)(-2)) )/(2(6)) \ = \ (5\pm√(577) )/(12) \ = \ 2.42, -1.58`

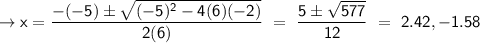
Solve for y : 2(2.42)² - 5(2.42) -7 and 2(-1.58)² - 5(-1.58) - 7 = -7.4, 5.9

Coordinates: (2.42,-7.4) and (-1.58, 5.9)