Answer:

Explanation:
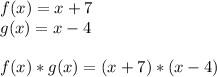
To solve a multiplication of 2 parenthesis, we'll multiply each of the terms on the left with each of the terms on the right. Then, add all of the products together.
First, x (left) with x (right):
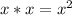
Next, x (left) with -4 (right):
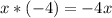
Next, 7 (left) with x (right):
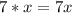
Finally, 7 (left) with -4 (right):
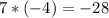
Now we have 4 products. To find the result of the entire expression, we need to add all of these together.
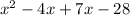
We can simplify -4x+7x to 3x:
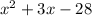
Answer:
