Answer:
-26 m/s.
Step-by-step explanation:
Hello,
In this case, since the vertical initial velocity is 26 m/s and the vertical final velocity is 0 m/s at P, we compute the time to reach P:
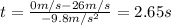
With which we compute the maximum height:
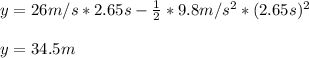
Therefore, the final velocity until the floor, assuming P as the starting point (Voy=0m/s), turns out:
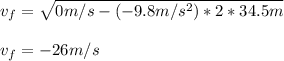
Which is clearly negative since it the projectile is moving downwards the starting point.
Regards.