Question

22. The sum of the first n terms of the arithmetical progression 3, 5.5, 8. .... is equal to the 2nth term of the arithmetic

progression 33/2, 57/2, 81/2. calculate n
[I.S.C
​

Answer 1

Given that,

Series 1: 3, 5.5, 8..... and series 2: 33/2, 57/2, 81/2.

To find,

The value of n.

Solution,

Let n is the no of terms in both the series.

For 3, 5.5, 8

First term, a = 3 and common difference d = 2.5

Sum of n terms of a series is given by :

`S=(n)/(2)(2a+(n-1)d)`

So,

`S=(n)/(2)(2* 3+(n-1)2.5)\\\\S=(n)/(2)(6+2.5(n-1))\ ....(1)`

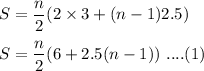
For 33/2, 57/2, 81/2

First term, a = 33/2 and common difference, d = 12

nth term of a series is given by :

`a_n=a+(n-1)d`

For 2nd terms,

`a_2=(33)/(2)+(2-1)* 12\ ....(2)`

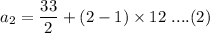
According to question, sum of the first n terms of the arithmetical progression 3, 5.5, 8. .... is equal to the 2nth term of the arithmetic progression 33/2, 57/2, 81/2

From equation (1) and (2) :

`(n)/(2)(6+2.5(n-1))=(33)/(2)+ 12\\\\(n)/(2)(6+2.5(n-1))=(57)/(2)\\\\n(6+2.5(n-1))=57\\\\6n+2.5n^2-2.5n-57=0\\\\2.5n^2+2.5n-57=0\\\\\text{On solving the above quadratic equation, we get the value of x as follows :}\\\\x=4.126,-5.526`

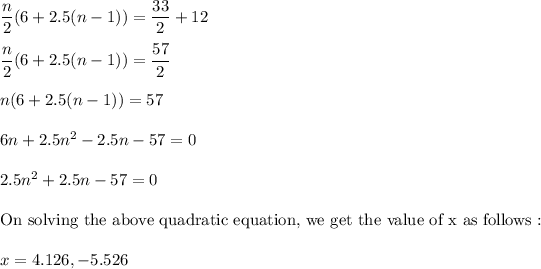
Neglecting the negative value, we get the value of n = 4.126

or

n = 4

Hence, the value of n is 4.