Question

Given RT below, if S lies on RT such that the

ratio of RS to ST is 3:1, find the coordinates
of S.

Answer 1

(-2, -3)

Explanation:

If a segment having extreme ends as
`(x_1,y_1)` and
`(x_2,y_2)` is divided by a point (x, y) in the ratio of m:n,

x =
`(mx_2+nx_1)/(m+n)`

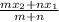
y =
`(my_2+ny_1)/(m+n)`

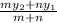
Since, a line RT has extreme ends as R(-5, 3) and T(-1, -5) then a point S(x, y) which divides RT in the ratio of 3 : 1 will be,

x =
`(3(-1)+1(-5))/(3+1)`

=
`(-8)/(4)`

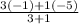
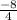
= -2

y =
`(3(-5)+1(3))/(3+1)`

=
`-(12)/(4)`

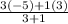
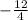
= -3

Therefore, coordinates of the point S will be (-2, -3).