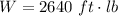Answer:
The value is
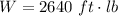
Explanation:
From the question we are told that
The weight of the bucket is
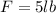
The depth of the well is
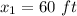
The weight of the water is

The rate at which the bucket with water is pulled is
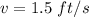
The rate of the leak is
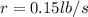
Generally the workdone is mathematically represented as
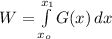 ]
]
Here G(x) is a function defining the weight of the system (water and bucket ) and it is mathematically represented as
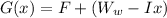
Here I is the rate of water loss in lb/ft mathematically represented as

=>
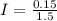
=>
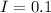
So
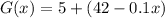
=>

So
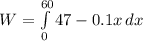 ]
]
=>
![W = [47x - (0.1x^2)/(2) ]|\left 60} \atop {0}} \right.](https://img.qammunity.org/2021/formulas/mathematics/college/s4k614ndickss5uiclch81hvtao6qx23sq.png)
=>
![W= [47(60) - 0.05(60)^2]](https://img.qammunity.org/2021/formulas/mathematics/college/3w1aq57im1rfjbm21899tdeovafie15wq3.png)
=>