Answer:
Explanation:
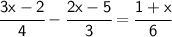
First, let's find the LCM of 4, 3, and 6.
How to find the LCM:
→ List multiples of each number.
→ Find the smallest number on each list.
4: 4, 8, 12, 16, 20, 24..
3: 3, 6, 9, 12, 15, 18, 21, 24, 27....
6: 6, 12, 18, 24, 30, 36, 42...
LCM: 12
_________
Now, we'll Multiply by LCM:
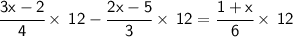
Simplify:
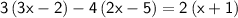
Now, expand, Apply the Distributive property:


Combine like terms:
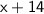
________
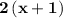
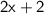
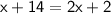
Subtract 14 from both sides:
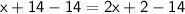
Simplify:
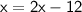
Subtract 2x from both sides:
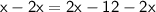
Simplify:
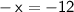
Divide both sides by -1:
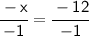
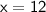
____________________________