Explanation:
Equation to find the sum of the first n terms :
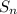 =
=
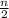 x (2
x (2
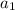 + (n - 1)d)
+ (n - 1)d)
- where n is the first n terms
- where
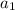 is the first term in the sequence
is the first term in the sequence
- where d is the difference (To find the difference:
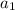 -
-
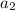 )
)
How to find n for the given sum :
1. Using the previous equation, plug in all the numbers that you know
2. PEMDAS then combine all like terms
3. Distribute what's on the outside to the inside of the parenthesis
4. Move
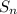 to the other side to make a quadratic equation
to the other side to make a quadratic equation
5. Solve the quadratic, then use the positive number and round that number (term of numbers that isn't whole isn't possible ig??)
Question 1:
Sum of first 10 terms :
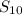 =
=
 ( 2 x 2 + (10 - 1)6)
( 2 x 2 + (10 - 1)6)
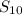 =
=
 (4 + (9)6) = (4 + 54) = 58
(4 + (9)6) = (4 + 54) = 58
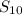 =
=
 x 58
x 58
Answer : 290
Find n for the given sum : 1704 =
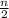 x (2 x 2 + (n - 1)6)
x (2 x 2 + (n - 1)6)
distribute 6 into (n-1)
1704 =
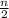 x ( 4 + 6n - 6)
x ( 4 + 6n - 6)
combine like terms
1704 =
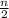 x ( -2 + 6n )
x ( -2 + 6n )
Distribute
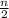 to ( -2 + 6n )
to ( -2 + 6n )
1704 =
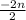 -
-
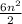
Simplify fractions and move 1704 to the other side
-3
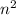 - n + 1704 = 0
- n + 1704 = 0
Use a quadratic calculator to find the answer and use the answer with the whole number
Answer : -24
Question 2:
(i'm just gonna show you the answers for the rest of them-)
Sum of the first 14 terms: 490
Find n for the given sum: 33.65 (I'm gonna round it to 34)
Question 3:
Sum of the first 21 terms: 483
Find n for the given sum: 11.48 (rounded: 11)
Question 4:
Sum of the first 32 terms: -1328
Find n for the given sum: -9.34 (rounded -9)
really hope this helps in any way :D