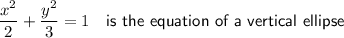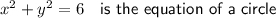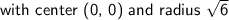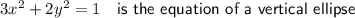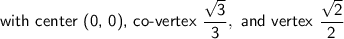Question

Here's the question, please help!

Answer 1

• x=2sint
• y=3sint

#1

• x²/2+y²/3
• (2sint)²/2+(3sint)²/3
• 4sin²t/2+9sim²t/3
• 2sin²t+3sim²t
• 5sin²t

False

#2

• x²+y²
• 4sin²t+9sin²t
• 13sin²t

False

#3

• 3x²+2y²
• 3(4sin²t)+2(9sin²t)
• 12sin²+18sin²t
• 30sin²t

False

None of the above

Answer 2

None of these

Explanation:

To convert the parametric curve into Cartesian form,
rewrite the equation for
`x` to make
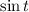`\sin t` the subject:

`x=2\sin t`

`\implies \sin t=(x)/(2)`

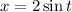
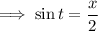
Substitute this into the given equation for
`y`:

`\begin{aligned}y & =3 \sin t\\\implies y & = 3 \left((x)/(2)\right)\\y& = (3)/(2)x\end{aligned}`

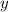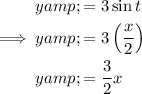
Therefore, the Cartesian form of the parametric curve is:

`y=(3)/(2)x`

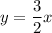
Further Information

`(x^2)/(2)+(y^2)/(3)=1 \quad \textsf{is the equation of a vertical ellipse}`

`\textsf{with center (0, 0), co-vertex }\sf √(2), \textsf{ and vertex }√(3)`

`x^2+y^2=6 \quad \textsf{is the equation of a circle}`

`\textsf{with center (0, 0) and radius }\sf √(6)`

`3x^2+2y^2=1 \quad \textsf{is the equation of a vertical ellipse}`

`\textsf{with center (0, 0), co-vertex }\sf (√(3))/(3), \textsf{ and vertex }(√(2))/(2)`