Question

2. Suppose that P(A) = 0.32, P(B) = 0.46, P(C) = 0.23, P(A ∪ B) = 0.57, P(A ∪ C) = 0.55, P(B ∪ C) = 0.49. a. Compute P(B ′ ). b. Compute P(A ∩ B), and use the result to determine if A and B are mutually exclusive. c. Determine if A and C are mutually exclusive. Explain briefly. d. Describe in simple words what (A ∪ B ∪ C)′ represents. Determine P[(A ∪ B ∪ C)′]. (Hint: Determine first P(B ∩ C).)

Answer 1

Explanation:

From the given information:

a.

Compute
`P(B')`:

`P(B') = 1 - P(B) \\ \\P(B') = 1 - 0.46 \\ \\ P(B') = \mathbf{0.54}`

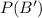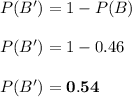
b.

Compute P(A ∩ B)

P(A ∩ B) = P(A) +P(B) - P(A∪B)

P(A ∩ B) = 0.32 + 0.46 - 0.57

P(A ∩ B) = 0.21

Thus, since P(A ∩ B) ≠ 0, we can say that they are not mutually exclusive.

c.

P(A ∩ C) = P(A) +P(C) - P(A∪C)

P(A ∩ C) = 0.32 + 0.23 -0.55

P(A ∩ C) = 0

Thus, since P(A ∩ C) = 0, we can say that they are both mutually exclusive.

d. To determine P[(A ∪ B ∪ C)′]

i.e. none of the events occurring

Then :

P(B ∩ C) = 0.46 +0.23 -0.49

P(B ∩ C) = 0.20

Therefore:

P(A ∪ B ∪ C) = P(A) + P(B) + P(C) - P(A ∩ B ) - P(A ∩ C) - P(B ∩ C) + P(A ∩ B ∩ C)

P(A ∪ B ∪ C) = 0.32 + 0.46 + 0.23 - 0.21 - 0 - 0.20 + 0

P(A ∪ B ∪ C) = 0.60