Answer:
(a)
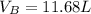
(b)
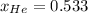
Step-by-step explanation:
Hello,
In this case, since the both gases behave ideally, with the given information we can compute the moles of He in A:

Thus, since the final pressure is 3.60 bar, we can write:

The moles of helium could be computed via solver as:
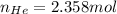
Or algebraically:

In such a way, the volume of the compartment B is:
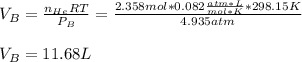
Finally, he mole fraction of He is:
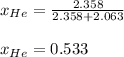
Regards.