Question

Consider the following algorithm: ```c++ Algorithm Mystery(n) { // Input:A nonnegative integer n S = 0; for i = 1 to n do { S = S + i * i; } return S } ``` 1. What does this algorithm compute? 2. What is its basic operation? 3. How many times is the basic operation executed? 4. What is the efficiency class of this algorithm? 5. Suggest an improvement, or a better algorithm altogether, and indicate its efficiency class. If you cannot do it, try to prove that, in fact, it cannot be done.

Answer 1

See explanation

Step-by-step explanation:

First let us find what this algorithm compute:

Algorithm Mystery(n) {

S = 0;

for i = 1 to n do

{ S = S + i * i; }

return S }

1)

Let suppose n = 3

S = 0

The algorithm has a for loop that has a loop variable i initialized to 1

At first iteration:

i = 1

S = S + i * i;

= 0 + 1 * 1

S = 1

At second iteration:

i = 2

S = 1

S = S + 2 * 2;

= 1 + 2 * 2

= 1 + 4

S = 5

At third iteration:

i = 3

S = 5

S = S + 3 * 3;

= 5 + 3 * 3

= 5 + 9

S = 14

Now the loop breaks at i=4 because loop iterates up to n and n =3

So from above example it is clear that the algorithm computes the sum of squares of numbers from 1 to n. Or you can say it compute the sum of first n squares. Let us represent this statement in mathematical form:

∑
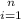`\left \ {{n} \atop {i=1}} \right.` i²

2)

From above example we can see that the basic operation is multiplication. At every iteration loop variable i is multiplied by itself from 1 to n or till n times. However we can also say that addition is the basic operation because at each iteration the value of S is added to the square of i. So it takes the same amount of time.

3)

In the for loop, the basic operation executes once. We can say that at each iteration of the loop, multiplication is performed once. Suppose A(n) represents the number of times basic operation executes then,

A(n) = ∑
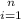`\left \ {{n} \atop {i=1}} \right.` 1 = n

4)

Since for loop executes once for each of the numbers from 1 to n, so this shows that for loop executes for n times. The basic operation in best, worst or average case runs n times. Hence the running time of Θ(n) . We can say that A(n) = n ∈ Θ(n)

If b is the number of bits needed to represent n then

b = log₂n + 1

b = log₂n

So

n ≈
`2^(b)`

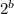
A(n) ≈
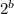`2^(b)` ≈ Θ(
`2^(b)` )

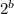5)

One solution is to calculate sum of squares without using Θ(n) algorithm. So the efficient algorithm that takes less time than the previous algorithm is:

Algorithm Mystery(n) {

S = 0;

S = (n * ( n + 1 ) (2n + 1) ) / 6 ;

return S}

Now the sum can be calculated in Θ(1) times. This is because regardless of the size and number of operands/operations, the time of arithmetic operation stays the same. Now lets find out how this algorithm works for

n = 3

S = (n * ( n + 1 ) (2n + 1) ) / 6 ;

= (3 * ( 3 + 1 ) * (2(3) + 1) ) / 6

= (3 * (4) * (6+1)) / 6

= (3 * (4) * (7)) / 6

= (3 * 4 * 7) / 6

= 84 / 6

S = 14