Answer:
6
Explanation:
The system of equations:
cx + 3y = c - 3 ... (i)
12x + cy = c ... (ii)
Multiplying (i) by c and (ii) by 3 gives;
c²x + 3cy = c² - 3c ... (i)
36x + 3cy = 3c ... (ii)
(i) - (ii) gives;
c²x - 36x + 0 = c² - 3c - 3c
c²x - 36x = c²
c²x - c² = 36x
c²(x - 1) = 36x
c² =
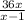
If c = -2 then;
(-2)² = 4 =
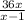 , 4x - 4 = 36x , 32x = -4 , x =
, 4x - 4 = 36x , 32x = -4 , x =
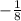
If c = 2 then;
2² =
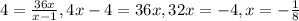
If c = 6 then;
6² = 36 =
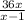 , 36x - 36 = 36x, 36x - 36x = 36 , x (36 - 36) = 36 , x(0) = 36 , x =
, 36x - 36 = 36x, 36x - 36x = 36 , x (36 - 36) = 36 , x(0) = 36 , x =
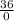 = undefined or infinitely many solutions.
= undefined or infinitely many solutions.
Hence the system of equations given above will have infinitely many solutions if the value of c is 6.