Question

For 7 and 8, find the maximum or minimum point of the parabola​

Answer 1

Answer: 7) Max: y = 52

8) Min: y = -51

Explanation:

The Max/Min is the y-value of the intercept.

• Max is when the a-value is negative.
• Min is when the a-value is positive.

First, find the x-value of the vertex using the Axis of Symmetry formula:

x = -b/2a. Then plug the x-value into the equation to find the y-value.

7) y = -2x² - 16x + 20

↓ ↓ ↓

a= -2 b= -16 c=20

`\text{AOS:}\quad x=(-b)/(2a)\quad =(-(-16))/(2(-2))\quad =(16)/(-4)\quad =-4`

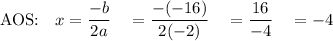
Max: y = -2(-4)² - 16(-4) + 20

= -2(16) + 64 + 20

= -32 + 84

= 52

*********************************************************************************************

7) y = x² + 12x - 15

↓ ↓ ↓

a= 1 b= 12 c= -15

`\text{AOS:}\quad x=(-b)/(2a)\quad =(-(12))/(2(1))\quad =(-12)/(2)\quad =-6`

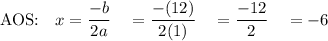
Max: y = (-6)² + 12(-6) - 15

= 36 - 72 - 15

= 36 - 87

= -51