Question

4. Find (f◦g)(x) and (g◦f)(x) and the domain of each.
​f(x)=x+3​, ​g(x)=

Answer 1

Answers:

`(f \circ g)(x) = 2x^2-5x\\\\(g \circ f)(x) = 2x^2+7x\\\\`

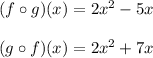
The domain is "all real numbers" which you could type in (-infinity, infinity) or
`(-\infty, \infty)` when doing interval notation. This applies to both.

=========================================================

Explanation:

See the attached image for the steps of each.

The domain is the set of all real numbers because each result is a polynomial. We don't have to worry about dividing by zero, taking a square root of a negative number etc. There are no restrictions on x. Any real number can replace x to get some real number result for y. This applies to both composite functions.