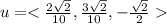Question

Let a=<-4,-3,5> Find a unit vector in the same direction as having positive first coordinate.

Answer 1

The value is
`u = < (2√(2))/(10) , (3√(2))/(10) , - (√(2))/(2)>`

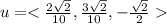
Explanation:

From the question we are told that

The vector is a=<-4,-3,5>

Generally the unit vector is
`u = ay`

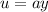
Here y represent the y-coordinate

So

`u =y <-4,-3,5>`

=>
`u = <-4y,-3y,5y>`

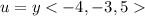
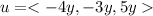
Generally the resultant of a unit vector is 1

So

`|u| = √( (-4y)^2 + (-3y)^2 + (5y)^2) = 1`

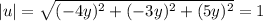
Hence

`|u| = √( 16y^2 + 9y^2 + 25y^2) = 1`

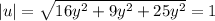
Taking the square of both sides

`16y^2 + 9y^2 + 25y^2 = 1`

=>
`50y^2 = 1`

=>
`y = \pm (1)/(√(50))`

=>
`y = \pm (1)/(5 √(2))`

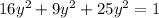
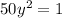
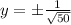
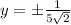
Rationalizing

=>
`y = \pm (√(2))/(10)`

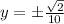
Given that the first coordinate is positive

`y = - (√(2))/(10)`

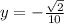
Hence the unit vector is

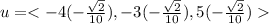
`u = <-4(- (√(2))/(10)),-3(- (√(2))/(10)),5(- (√(2))/(10))>`

=>
`u = < (2√(2))/(10) , (3√(2))/(10) , - (√(2))/(2)>`