Question

O A. Function fis even.

ОВ.
Function fis neither even nor odd.
O C.
Function fis both even and odd.
D.
Function fis odd.
F(x)= -8x^5+4x^3+5x

Answer 1

D) Function f is odd

Explanation:

There are three ways to solve this problem:

Method 1

Recall that a function is even if
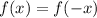`f(x)=f(-x)` and odd if
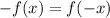`-f(x)=f(-x)` for all x. Hence, we evaluate
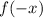`f(-x)` to check if the function is even, odd, both, or neither:

`f(x)=-8x^5+4x^3+5x\\\\f(-x)=-8(-x)^5+4(-x)^3+5(-x)\\\\f(-x)=8x^5-4x^3-5x`

Here, we can see that the signs of the original terms switched to their opposite operations, so it is clear that
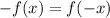`-f(x)=f(-x)`, which tells us that the function is odd.

Method 2

A function is odd if it has symmetry about the origin, and even if it has symmetry about the y-axis. We can clearly see on the graph there is origin symmetry, so the function is odd.

Method 3

A function is even if every term in that function has an even degree, or odd if every term has an odd degree. We can see that the degrees of each term are odd, so we can conclude that the function is odd.