Question

Hi! I was wondering if you could help with this question please :)​

Answer 1

`R=(QJ)/(I^2t)`

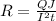
Explanation:

So we have the equation:

`Q=(I^2Rt)/(J)`

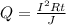
And we want to solve for R.

First, let's multiply both sides by J to remove the fraction on the right. So:

`(J)Q=(J)(I^2Rt)/(J)`

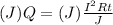
Simplify the right:

`JQ=I^2Rt`

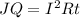
We can rewrite our equation as:

`JQ=R(I^2t)`

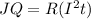
So, to isolate the R variable, divide both sides by I²t:

`(JQ)/(I^2t)=(R(I^2t))/(I^2t)`

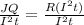
The right side cancels, so:

`R=(QJ)/(I^2t)`

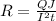
And we are done!