Question

Find the length of segment DE.

Answer 1

The length of segment DE is
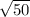`\( √(50) \)`units.

Explanation:

To find the length of segment DE, we typically use the distance formula, which is derived from the Pythagorean theorem in a Cartesian coordinate system. The formula is
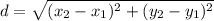`\(d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)\)`, representing the distance between two points (x1, y1) and (x2, y2). Unfortunately, specific coordinates for points D and E are not provided in the question.

Without knowing the exact coordinates, we can't perform a numerical calculation. However, we can express the length of segment DE in terms of the square root of the sum of squared differences between the x and y coordinates. In this case,
`\(d = √(50)\)` units.

The square root of 50 cannot be simplified further since 50 is not a perfect square. This value represents the magnitude of the displacement vector between points D and E. It is crucial to have coordinate values to perform an accurate numerical calculation. If given, the coordinates could be substituted into the distance formula to find the precise length of segment DE.

Question:

To find the length of segment DE, I would need additional information such as the coordinates or description of points D and E in a coordinate plane, the type of geometric figure or context in which these points are located, or any given measurements or relationships provided in the problem. Please provide more details or context so that I can assist you in finding the length of segment DE accurately.

Answer 2

segments forming a square at the vertex