Given:
Two numbers are
 and
and
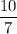 .
.
To find:
A repeating decimal that is between
 and
and
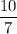 .
.
Solution:
Using calculator, we get
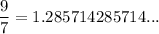
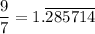
and,
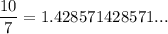
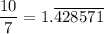
Now, the repeating decimal that is between
 and
and
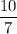 be x. So,
be x. So,
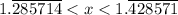
On analyzing the numbers to hundredth places, we get 1.28 < 1.33 < 1.42, therefore
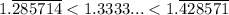
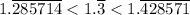
And we know that
 is the decimal form of
is the decimal form of
 .
.
Therefore, the required number is
 .
.