Question

An airplane travels at 300 mi/h south for 2.00 h and then at 250 mi/h north for 750 miles. What is the average speed for the trip? Group of answer choices

Answer 1

270 mi/h

Step-by-step explanation:

Given that,

To the south,

v₁ = 300 mi/h, t₁ = 2 h

We can find distance, d₁

`d_1=v_1* t_1\\\\d_1=300* 2\\\\d_1=600\ \text{miles}`

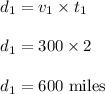
To the north,

v₂ = 250 mi/h, d₂ = 750 miles

We can find time, t₂

`t_2=(d_2)/(v_2)\\\\t_2=\frac{750\ \text{miles}}{250\ \text{mi/h}}\\\\t_2=3\ h`

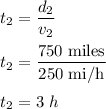
Now,

Average speed = total distance/total time

`V=(d_1+d_2)/(t_1+t_2)\\\\V=(600+750)/(2+3)\\\\V=270\ \text{mi/h}`

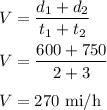
Hence, the average speed for the trip is 270 mi/h.