Question

You're trying to predict whether it will rain on the day of your child's birthday party. The party is at a park. If it doesn't rain, then you can sit in the grass to eat. If it does rain, sitting in the grass will be very unpleasant, and you'd prefer to sit at the sheltered tables. But, the shelter costs $100 to reserve, and you have to decide 1 week ahead you can't just wait to see the actual weather before deciding. Assume you can't use the shelter if you don't reserve it. You quantify your loss in different scenarios as the loss function L(y,g), where y=1 if it actually rains and y=0 if not, and g is your guess: L(1,1)=L(0,0)=0, and L(0,1)=100, L(1,0)=500. Let P(Y=1)=0.1. Then, your optimal prediction is g=

Answer 1

the minimal loss of the optimal prediction would be g = 0

Explanation:

From the given question, we formulate y and g to be:

`y =\begin{cases} 1, & \text{rain with probability 0.1} \\ 0, & \text{rain with probability 0.9} \end{cases}`

`g =\begin{cases} 1, & \text{if we guess it will rain} \\ 0, & \text{if we guess it will not rain} \end{cases}`

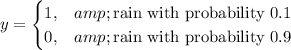
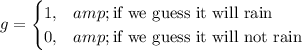
Loss function = L(y.g)

The expected loss for g = 1 & g = 0 can now be determined as follows:

When g = 1; ( i.e. guess it will rain)

The expected loss = L(1,1) × Probability (y = 1) + L(0,1) × Probability (y = 0)

The expected loss = 0 × 0.1 + 100 × 0.9

The expected loss = $90

When g = 0; ( i.e. guess it will not rain)

The expected loss = L(1,0) × Probability (y = 1) + L(0,0) × Probability (y = 0)

The expected loss = 500 × 0.1 + 0 × 0.9

The expected loss = $50

Therefore, the minimal loss of the optimal prediction would be g = 0 i.e it will not rain on the day of the child's birthday.