Answer:
(a). The mean speed is 760 m/s.
(b). The standard deviation for our normal model is 142.1 m/s.
(c). The unusual speed is 1127 m/s.
(d). The average molecule speed is 929.48 m/s.
Explanation:
Given that,
Molecules in the air are moving with speeds based on the normal model.
Let x be the speed of the molecules.
(a). If half of the air molecules are moving faster than 760 m/s.
We can say speed of a molecules is normally distributed.
So, the mean, median and mode of this distribution is at least greater than 760 m/s.
(b). If exactly 95% of the molecules are moving with speeds between 475.8 m/s and 1044.2 m/s,
If the standard deviation is σ and the mean is μ,
We need to calculate the standard deviation for our normal model
Using empirical rule
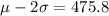 ...(I)
...(I)
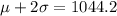 ....(II)
....(II)
Put the value of μ in equation (I)
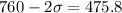
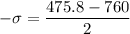
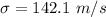
(c). One molecule is found to be moving with a speed of 1127 m/s.
We know that,
1127 is the between 1126 and 1128.
Since, it is a continuous distribution,
We need to find the probability that speed is between this
Using excel function
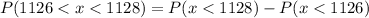
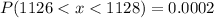
We know that,
Any probability less than 0.05 is considered as unusual
So, 0.0002<0.05
So, 1127 will be considered as the unusual speed.
(d). If the temperature increase caused the z-score of a particle moving at 1100 m/s particle to drop to 1.2 after the temperature increase.
We need to calculate the average molecule speed
Using formula of average molecule speed
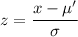
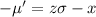
Put the value in to the formula
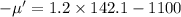

Hence, (a). The mean speed is 760 m/s.
(b). The standard deviation for our normal model is 142.1 m/s.
(c). The unusual speed is 1127 m/s.
(d). The average molecule speed is 929.48 m/s.