Question

You are working laboratory device that includes a on a CR small sphere with a large electric charge Q. Because of this charged sphere, there is a strong electric field surround- ing your device. Other researchers in your laboratory complaining that your electric field is affecting their equip- ment. You think about how you can obtain the large elec- tric field that you need close to the sphere but prohibit the field from reaching your colleagues. You decide to surround your device with a spherical transparent plastic shell. The nonconducting shell is given a uniform charge distribu- tion. (a) The shell is placed so that the small sphere is at the exact center of the shell. Determine the charge that must be placed on the shell to completely eliminate the electric field outside of the shell. (b) What if the shell moves? Does the small sphere have to be at the center of the shell for this scheme to work? sm at SC are ur la ca ch VC ve th th ti SI C

Answer 1

a) q_shell = -Q , b) q_shell = -Q

Step-by-step explanation:

a) We can solve this exercise using Gauss's law

Ф = ∫ E. dA =
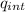`q_(int)` /ε₀

For this we use a Gaussian surface that takes advantage of the symmetry of the problem, we select a sphere that this force of the spherical plastic shell.

In this case the electric field lines coincide with the radii of the sphere and the scalar product reduces to the algebraic product, the area of ​​the sphere

A = 4 π r²

fi = E 4π r² = q_{int} /ε₀

apply this formula to our case, we have that the charge inside the Gaussian sphere is

q_{int} = q_sphere + q_shell

the charge of the sphere is Q and the requirement is that there is no electric field outside the Guasian sphere, for this the net charge inside it must be zero

0 = Q + q_shell

q_shell = -Q

b) In Gauss's law, only the charge inside the Gaussian surface matters, not its position, therefore if the charge is not in the center the result remains the same.

q_shell = -Q