Question

An insurance company divides its policyholders into low-risk and high-risk classes. 60% were in the low-risk class and 40% in the high-risk class. Of those in the low-risk class, 80% had no claims, 15% had one claim, and 5% had two claims. Of those in the high-risk class, 50% had no claims, 30% had one claim, and 20% had two claims. (Write answers as exact decimals.)

a) What is the probability that a randomly selected policyholder is high-risk and filed no claims?
b) What is the probability that a randomly selected policyholder filed two claims?

Answer 1

a). 0.294

b) 0.11

Explanation:

From the given information:

the probability of the low risk = 0.60

the probability of the high risk = 0.40

let
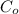`C_o` represent no claim

let
`C_1` represent 1 claim

let
`C_2` represent 2 claim :

For low risk;

so,
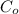`C_o` = (0.80 * 0.60 = 0.48),
`C_1` = (0.15* 0.60=0.09),
`C_2` = (0.05 * 0.60=0.03)

For high risk:

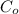`C_o` = (0.50 * 0.40 = 0.2),
`C_1` = (0.30 * 0.40 = 0.12) ,
`C_2` = ( 0.20 * 0.40 = 0.08)

Therefore:

a), the probability that a randomly selected policyholder is high-risk and filed no claims can be computed as:

`P(H|C_o) = (P(H \cap C_o))/(P(C_o))`

`P(H|C_o) = ((0.2))/((0.48+0.2))`

`P(H|C_o) = ((0.2))/((0.68))`

`P(H|C_o) = 0.294`

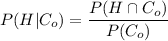
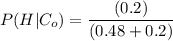
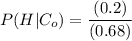
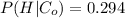
b) What is the probability that a randomly selected policyholder filed two claims?

the probability that a randomly selected policyholder be filled with two claims = 0.03 + 0.08

= 0.11