Answer:
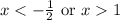
Explanation:
So we have the equation:

First, note that since the sign is greater than, this is an or inequality (not an "and" inequality). This is the student's first mistake.
So, let's solve this inequality.
Case 1:
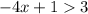
Subtract 1 from both sides:
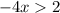
Divide both sides by -4:
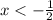
The student did not flip the sign when doing this step, hence the incorrect answer.
You correctly spotted the student's mistake. Nicely done!
Case 2:

This is what you're missing: for this second instance, we must flip the sign to less than right away. This is because we are essentially multiplying the 3 by a negative. So, we must flip the sign in order to be correct.
Now solve. Subtract 1 from both sides:
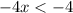
Divide both sides by -4. Since we're dividing by a negative, flip the sign:
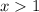
So, our solutions are:
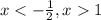
As mentioned previously, this is an or inequality. Therefore, our final answer is:
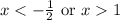
Edit: Improved Answer