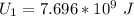Answer:
a
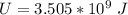
b
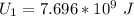
Step-by-step explanation:
From the question we are told that
The capacitance is
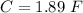
The voltage is

The first dielectric constant is

The second dielectric constant is
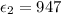
Generally the electric potential energy is mathematically represented as
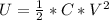
=>
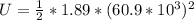
=>
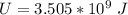
Generally the capacitance when the capacitor's filling was changed is

=>

Generally the electric potential energy when the capacitor's filling was changed is

=>

=>