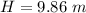Answer:
a
Generally from third equation of motion we have that
![v^2 = u^2 + 2a[s_i - s_f]](https://img.qammunity.org/2021/formulas/physics/high-school/gdbcykfz0tzzh5yiwn5hizj114oopit770.png)
Here v is the final speed of the car
u is the initial speed of the car which is zero
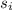 is the initial position of the car which is certain height H
is the initial position of the car which is certain height H
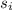 is the final position of the car which is zero meters (i.e the ground)
is the final position of the car which is zero meters (i.e the ground)
a is the acceleration due to gravity which is g
So
![v^2 = 0 + 2g[H - 0]](https://img.qammunity.org/2021/formulas/physics/high-school/ni55po7feiilaoeribl4ursdoxce7qvr0r.png)
=>
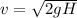
b
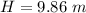
Step-by-step explanation:
Generally from third equation of motion we have that
![v^2 = u^2 + 2a[s_i - s_f]](https://img.qammunity.org/2021/formulas/physics/high-school/gdbcykfz0tzzh5yiwn5hizj114oopit770.png)
Here v is the final speed of the car
u is the initial speed of the car which is zero
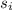 is the initial position of the car which is certain height H
is the initial position of the car which is certain height H
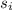 is the final position of the car which is zero meters (i.e the ground)
is the final position of the car which is zero meters (i.e the ground)
a is the acceleration due to gravity which is g
So
![v^2 = 0 + 2g[H - 0]](https://img.qammunity.org/2021/formulas/physics/high-school/ni55po7feiilaoeribl4ursdoxce7qvr0r.png)
=>
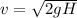
When
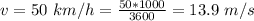 we have that
we have that
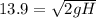
=>
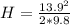
=>