Question

Why it is not necessary to use the distance formula for vertical or horizontal segments

Answer 1

The distance of vertical segments is found from the difference between the y-coordinate values, distance = y₂ - y₁

The distance for horizontal segments is found from the difference between the x-coordinate values, distance = x₂ - x₁

Explanation:

The distance formula for finding the distance between two points with the given coordinates, (x₁, y₁), (x₂, y₂) can be presented as follows;

`Distance =\sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}`

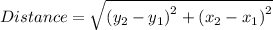
For vertical segments, we have that the values of the x-coordinates are the same for both points, such as x₁ = x₂ which gives the distance between the points as follows;

`Distance =\sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)} \\\\ (x_1 = x_2) \\ \\\therefore Distance = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(2) \right )^(2)} =\sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (0 \right )^(2)}\\\\Distance =\sqrt{\left (y_(2)-y_(1) \right )^(2)} = y_(2)-y_(1)`

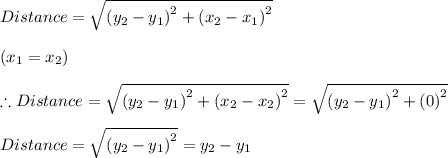
Therefore, the distance of vertical segments is found by simply finding the difference between the y-coordinate values, distance = y₂ - y₁

Similarly, for horizontal segments, we have the values of the y-coordinates are the equal for both points, such as y₁ = y₂ which gives the distance between the points as follows;

`Distance =\sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)} \\\\ (y_1 = y_2) \\ \\\therefore Distance = \sqrt{\left (y_(2)-y_(2) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)} =\sqrt{\left (0 \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}\\\\Distance =\sqrt{\left (x_(2)-x_(1) \right )^(2)} = x_(2)-x_(1)`

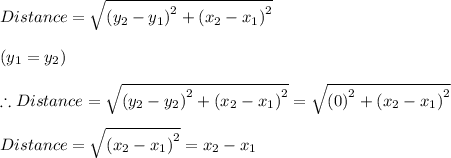
The distance of horizontal segments is the difference between the x-coordinate values, distance = x₂ - x₁.