Question

Find the surface area of the right triangular prism (above) using its net (below)

Answer 1

`96 \text{ units}^2`

Explanation:

I attached a diagram numbering each side to make it a bit easier to refer to them.

Let's start by calculating the area of the two triangles (2)

Typically the area of a triangle is calculated as:
`(1)/(2)bh`, where b=base, and h=height.

In this case, we don't have to divide by 1/2, since we have two triangles, so there sum, will add to:
`bh`, because if you align them, you actually form a rectangle!

In the diagram it's given that the base is 4, and the height is 3, so the area of both triangles is:
`12 \text{ units}^2`

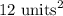
Now let's calculate the area of the rectangle in the back (1)

The dimensions are given as 3 and 7, and we can simply calculate the area by multiplying these two dimensions, to get:
`21\text{ units}^2`

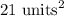
Now let's calculate the rectangle on the bottom (3), its units are given as 4 and 7, and we can multiply these two to get an area of:
`28 \text{ units}^2`

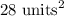
Now let's calculate the slanted rectangle (4), its units are given as 5 and 7, which can multiply to get an area of:
`35 \text{ units}^2`

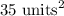
Now to find the surface area of the entire thing, we simply add these values.

`12 \text{ units}^2 +21 \text{ units}^2 + 28 \text{ units}^2 + 35 \text{ units}^2 = 96 \text{ units}^2`

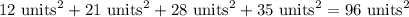
which is our answer!