Question

A child on a bridge throws a rock straight down to the water below. The point where the child released the rock is 74 m above the water and it took 2.7 s for the rock to reach the water. Determine the rock's velocity (magnitude & direction) at the moment the child released it. Also determine the rock's velocity (magnitude & direction) at the moment it reached the water. Ignore air drag.

Answer 1

The rock's altitude y at time t, thrown with initial velocity v, is given by

`y=74\,\mathrm m+vt-\frac12gt^2`

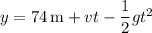
where
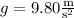`g=9.80(\rm m)/(\mathrm s^2)` is the acceleration due to gravity.

After t = 2.7 s, the rock reaches the water (0 altitude), so

`0=74\,\mathrm m+v(2.7\,\mathrm s)-\frac12g(2.7\,\mathrm s)^2`

`\implies v=-(74\,\mathrm m-\frac g2(2.7\,\mathrm s)^2)/(2.7\,\mathrm s)\approx-14.177(\rm m)/(\rm s)`

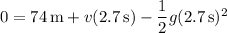
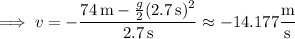
so the rock was thrown with a velocity with magnitude 14 m/s and downward direction.

Its velocity at time t is
`v-gt` (with no horizontal component), so that at the moment it hits the water, its velocity is

`v-g(2.7\,\mathrm s)\approx-40.637(\rm m)/(\rm s)`

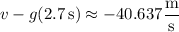
That is, its final velocity has an approximate magnitude of 41 m/s, also directed downward.