Answer:
v = 8.03 m / s
Step-by-step explanation:
This is a missile throwing exercise.
y = y₀ +
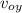 t - ½ g t²
t - ½ g t²
indicates that y = -1.2 m and the initial velocity is
v_{oy} = v₀ sin θ
v_{oy} = 6.4 sin 2.2
v_{oy} = 0.2457 m / s
we substitute in the equation
-1.2 = 0.2457 t - ½ 9.8 t²
4.9 t² - 0.2457 t - 1.2 = 0
t² - 0.05014 t -0.2449 = 0
we solve the quadratic equation
t = [0.05014 ±√ (0.05014² + 4 0.2449)] / 2
t = [0.05014 ± 0.9910] / 2
t₁ = 0.5206 s
t₂ = -0.47 s
time must be a positive magnitude therefore the correct answer is
t = 0.5206 s
with this time we can calculate the vertical speed when the rock hits the ground
v_{y} = v_{oy} - gt
v_{y} = 0.2457 - 9.8 0.5206
v_{y} = -4.856 m / s
the negative sign indicates that the speed is down
horizontal velocity is constant, due to no acceleration
vₓ = v₀ₓ = v₀ cos 2,2
v₀ₓ = 6.4 cos 2.2
v₀ₓ = 6.395 m / s
therefore let's use Pythagoras' theorem to find the velocity
v = √ (vₓ² +
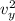 )
)
v = √ (6,395² + 4,856²)
v = 8.03 m / s
the direction can be found with trigonometry
tan θ = v_{y} / vₓ
θ = tan⁻¹ (-4,856 / 6,395)
θ = - 37
the negative sign indicates that it is half clockwise from the x axis