Question

Two chords measuring 18.64cm and 14.32cm intersect at a point on a circle at an angle of 114°26’. A third chord connects the noncommon endpoints of the chords to form a triangle. Find all the measurements of the triangle.

Answer 1

third chord length is 27.8088 cm

Between III and I chord is
`27^\circ57'30''`

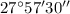
Between III and II chord is
`37^\circ36'30''`

Explanation:

The calculation of measurements of the triangle is shown below:-

By Cosine rule

`BC^2 = (14.32)^2 + (18.64)^2 - 2* 14.32 * 18.64 cos\114^\circ26'\\\\ BC^2 = 773.330156\\\\ BC = √(773.330156)`

BC = 27.8088 (it is the length of third chord)

By Sin rule

`(Sin A)/(BC) = (Sin B)/(14.32) \\\\ (Sin114^\circ26')/(27.8088) = (Sin B)/(14.32) \\\\ Sin B = (14.32114^\circ26)/(27.8088)`

After solving this we will get

Sin B = 0.468829

`<B = Sin^(-1) 0.468829\\\\ <B = 27^\circ 57'30''`

Therefore

`<A + <B + <C = 180^\circ`

`<C = 180^\circ - 114^\circ26'-27^\circ57'30''\\\\ <C = 37^\circ36'30''`

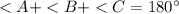
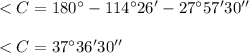
Now,

third chord length is 27.8088 cm

Between III and I chord is
`27^\circ57'30''`

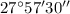
Between III and II chord is
`37^\circ36'30''`

The same is to be considered