Question

John invests $3,000 into an account that earns 4.7% interest compounded quarterly. Write an equation and us it to find the value of John’s investment after 12 years

Answer 1

Given:

Principal = $3000

Rate of interest = 4.7% = 0.047 compounded quarterly.

Time = 12 yeas

To find:

The value of John’s investment after 12 years.

Solution:

The formula for amount is

`A=P\left(1+(r)/(n)\right)^(nt)`

where, P is principal, r is rate of interest, n is number of times interest compounded in an year, t is number of years.

Substitute P=3000, r=0.047, n=4 and t=12 in the above formula.

`A=3000\left(1+(0.047)/(4)\right)^(4(12))`

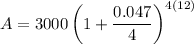
Therefore, the required equation is
`A=3000\left(1+(0.047)/(4)\right)^(4(12))`.

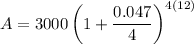We can further solve this.

`A=3000\left(1+0.01175 \right)^(48)`

`A=3000\left(1.01175 \right)^(48)`

`A=5255.75947323`

`A\approx 5255.76`

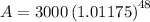
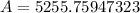
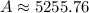
Therefore, the value of John’s investment after 12 years is $5255.76.