Question

What is the perimeter of the rectangle with length of 2x + 3 and width of 5x - 5? Explain your process to find the perimeter

Answer 1

Perimeter means length of the boundary.

The length of the boundary of a rectangle includes the sum of 2 lengths and 2 breadths. So, we can write the perimeter of rectangle as:

`\large{ \boxed{ \bf{p = 2(l + b)}}}`

Where,

• P = Perimeter
• l = length
• b = breadth

In the question,

It's given that l = 2x + 3 and b = 5x - 5

So, let's find the perimeter by using the formula,

⇛ P = 2[ (2x + 3) + (5x - 5)]

⇛ P = 2(2x + 3 + 5x - 5)

⇛ P = 2(7x - 2)

Opening the parentheses,

⇛ P = 14x - 4

Perimeter of the rectangle:

`\large{ \boxed{ \bf{ \red{p = 14x - 4}}}}`

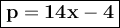
And we are done !!

#CarryOnLearning

━━━━━━━━━━━━━━━━━━━━