Question

If A, B ,C are the angles of a triangle then,
Please help me to prove this!​

Answer 1

Answer: see proof below

Explanation:

Given: A + B + C = π → A + B = π - C

→ C = π - (A + B)

Use the Cofunction Identities: sin (π/2 - A) = cos A

cos (π/2 - A) = sin A

Use the Double Angle Identity: cos 2A = 1 - 2 sin² A

Use Sum to Product Identity: cos A - cos B = 2 sin [(A+B)/2] · sin [(A-B)/2]

Proof LHS → RHS:

`\text{LHS:}\qquad \qquad \sin \bigg((A)/(2)\bigg)+\sin \bigg((B)/(2)\bigg)+\sin \bigg((C)/(2)\bigg)`

`\text{Given:}\qquad \quad \sin \bigg((A)/(2)\bigg)+\sin \bigg((B)/(2)\bigg)+\sin \bigg((\pi-(A+B))/(2)\bigg)\\\\\\.\qquad \qquad =\sin \bigg((A)/(2)\bigg)+\sin \bigg((B)/(2)\bigg)+\sin \bigg((\pi)/(2)-(A+B)/(2)\bigg)`

`\text{Cofunction:}\qquad \sin \bigg((A)/(2)\bigg)+\sin \bigg((B)/(2)\bigg)+\cos \bigg((A+B)/(2)\bigg)`

`\text{Sum to Product:}\quad 2\sin \bigg((A+B)/(2\cdot 2)\bigg)\cdot\cos \bigg((A-B)/(2\cdot 2)\bigg)+\cos \bigg((A+B)/(2)\bigg)`

`\text{Double Angle:}\qquad 2\sin \bigg((A+B)/(4)\bigg)\cdot\cos \bigg((A-B)/(4)\bigg)+1-2\sin^2 \bigg((A+B)/(2\cdot 2)\bigg)`

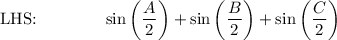
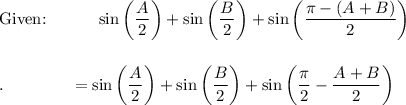
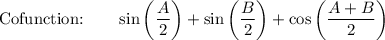
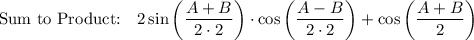
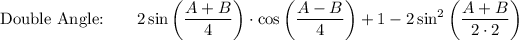
`\text{Factor:}\qquad \qquad 1+2\sin \bigg((A+B)/(4)\bigg)\bigg[\cos \bigg((A-B)/(4)\bigg)-\sin \bigg((A+B)/(4)\bigg)\bigg]`

`\text{Cofunction:}\qquad 1+2\sin \bigg((A+B)/(4)\bigg)\bigg[\cos \bigg((A-B)/(4)\bigg)-\cos \bigg((\pi)/(2)-(A+B)/(4)\bigg)\bigg]\\\\\\.\qquad \qquad \qquad =1+2\sin \bigg((A+B)/(4)\bigg)\bigg[\cos \bigg((A-B)/(4)\bigg)-\sin \bigg((2\pi -(A+B))/(4)\bigg)\bigg]`

`\text{Sum to Product:}\quad 1+2\sin \bigg((A+B)/(4)\bigg)\bigg[2 \sin \bigg((2\pi-2B)/(2\cdot 4)\bigg)\cdot \sin \bigg((2A-2\pi)/(2\cdot 4)\bigg)\bigg]\\\\\\.\qquad \qquad \qquad =1+4\sin \bigg((A+B)/(4)\bigg)\cdot \sin \bigg((\pi-B)/(4)\bigg)\cdot \sin \bigg((\pi -A)/(4)\bigg)`

`\text{Given:}\qquad \qquad 1+4\sin \bigg((\pi-C)/(4)\bigg)\cdot \sin \bigg((\pi-B)/(4)\bigg)\cdot \sin \bigg((\pi -A)/(4)\bigg)\\\\\\.\qquad \qquad \qquad =1+4\sin \bigg((\pi-A)/(4)\bigg)\cdot \sin \bigg((\pi-B)/(4)\bigg)\cdot \sin \bigg((\pi -C)/(4)\bigg)`

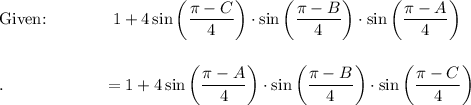
LHS = RHS
`\checkmark`