Question

I need help with this

Answer 1

8)2.86 cm^2

9) 100.48 m^2

10) 23.08 in^2

Explanation:

8) In the figure , there's a right angled triangle in which a circle of radius 1 cm is inscribed in that triangle.

Area of the right angled triangle =

`(1)/(2) * 4 * 3 = 6 \: {cm}^(2)`

Area of the circle =

`\pi {r}^(2) = \pi {(1)}^(2) = (22)/(7) = 3.14 \: {cm}^(2) </p><p>`

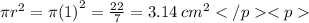
Area of the shaded portion ( although itz not shaded..... i mean remaining portion ) = 6 - 3.14 =2.86cm^2

9) In this figure there's a circle in which more 2 circles are inscribed in such a way that the center of the bigger circle is in the circumferences of both the circles.

Area of the bigger circle =

`\frac{\pi {d}^(2) }{4} = (\pi * 16 * 16)/(4) = 64\pi \\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: = 200.96 {m}^(2)`

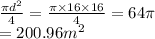
The small circles have equal diameter ( i.e. 8m) . So , Area of the small circles =

`2( \frac{\pi {d}^(2) }{4} ) = 2( \frac{\pi * {8}^(2) }{4} ) = 32\pi \\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: = 100.48 \: {m}^(2)`

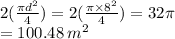
Area of the shaded region =

200.96 - 100.48 = 100.48 m^2

10) In the figure , the radius of the circle is 9 in.

So the area of a quarter =

`\frac{\pi {r}^(2) }{4} = \frac{\pi * {(9)}^(2) }{4} = (81\pi)/(4) = 63.58 \: {in}^(2)`

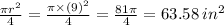
Also in that circle a right angled triangle is formed. Area of that right angles triangle =

`(1)/(2) * 9 * 9 = 40.5 \: {in}^(2)`

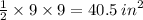
So the area of the region shaded =

63.58 - 40.5 = 23.08 in^2