- A ball is dropped from a height = H
- The total distance covered in last second of its motion is equal to the distance covered in first 3 second .
- The height of the journey .

We have know that,
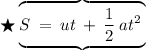
Where,
- u = initial velocity = 0m/s
[Note :- Here, acceleration is ‛acceleration due to gravity’ .]
=> S = 1/2 × 10 × (3)^2
=> S = 5 × 9
=> S = 45m -----(1)
✒ If the ball takes ‛n’ second to fall the ground, then distance covered in nth second is,
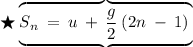
=> Sn = 0 + 10/2 (2 × n - 1)
=> Sn = 5 (2n - 1)
=> Sn = 10n - 5 -----(2)
Therefore,
=> 10n = 45 + 5
=> n = 50/10
=> n = 5
Now put the value of ‛n = 5’ in equation(2), we get
=> Sn = 10 × 5 - 5
=> Sn = 50 - 5
=> Sn = 45m
 The height of the journey is “ 45m ” .
The height of the journey is “ 45m ” .