Question

A tank with capactity 500 gal originally contains 200 gal water with 100 lbs of salt mixed into it. Water containing 1 lb of salt per gallon is entering at a rate of 3 gal/min, and is allowed to leave at 2 gal/min. Find the amount of salt in the tank at any time prior to the instant the tank overflows. Find the concentration (in pounds per gallon) of salt in the tank when it is at the point of overflowing. Compare this concentration with the theoretical limiting concentration if the tank had infinite volume.

Answer 1

The amount of salt in the tank at any moment
`t` is

`f(t)=-\frac {4* 10^6}{(200+t)^2}+200+t`

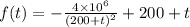
The concentration of salt in the tank when it is at the point of overflowing is
`0.968`.

The theoretical limiting concentration of an infinite tank is
`1` lb per gallon.

Explanation:

Let
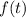`f(t)` be the amount of salt in the tank at any time
`t.`

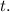
Then, its time rate of change,
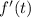`f'(t)`, by (balance law).

Since three gallons of salt water runs in the tank per minute, containing
`1`lb of salt, the salt rate is

`3.1=3`

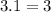
The amount of water in the tank at any time
`t` is.

`200+(3-2)t=200+t,`

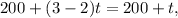
Now, the outflow is
`2` gal of the solution in a minute. That is
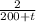`\frac 2{200+t}` of the total solution content in the tank, hence
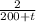`\frac 2{200+t}` of the salt salt content
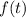`f(t)`, that is
`(2f(t))/(200+t)`.

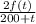Initially, the tank contains
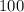`100` lb of salt,

Therefore we obtain the initial condition
`f(0)=100`

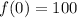
Thus, the model is

`f'(t)=3-(2f(t))/(200+t), f(0)=100`

`\Rightarrow f'(t)+(2)/(200+t)f(t)=3, f(0)=100`

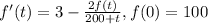
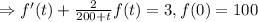
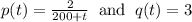`p(t)=(2)/(200+t) \;\;\text{and} \;\;q(t)=3` Linear ODE.

so, an integrating factor is

`e^(\int p dt)=e^{2\int (dt)/(200+t)=e^(\ln(200+t)^2)=(200+t)^2`

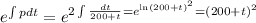
and the general solution is

`f(t)(200+t)^2=\int q(200+t)^2 dt+c`

`\Rightarrow f(t)=\frac 1{(200+t)^2}\int 3(200+t)^2 dt+c`

`\Rightarrow f(t)=\frac c{(200+t)^2}+200+t`

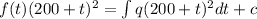
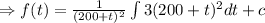
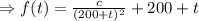
Now using the initial condition and find the value of
`c`.

`100=f(0)=\frac c{(200+0)^2}+200+0\Rightarrow -100=\frac c{200^2}`

`\Rightarrow c=-4000000=-4* 10^6`

`\Rightarrow f(t)=-\frac {4* 10^6}{(200+t)^2}+200+t`

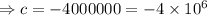
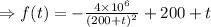
is the amount of salt in the tank at any moment
`t.`

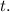
Initially, the tank contains
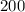`200` gal of water and the capacity of the tank is
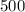`500` gal. This means that there is enough place for

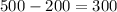`500-200=300` gal

of water in the tank at the beginning. As concluded previously, we have one new gal in the tank at every minute. hence the tank will be full in
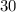`30`min.

Therefore, we need to calculate
`f(300)` to find the amount of salt any time prior to the moment when the solution begins to overflow.

`f(300)=-(4* 10^6)/((200+300)^2)+200+300=-16+500=484`

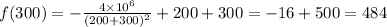
To find the concentration of salt at that moment, divide the amount of salt with the amount of water in the tank at that moment, which is
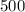`500`L.

`\text{concentration at t}=300=(484)/(500)=0.968`

If the tank had an infinite capacity, then the concentration would be

`\lim\limits_(t \to \infty) (f(t))/(200+t)= \lim\limits_(t \to \infty)\left(((3\cdot 10^6)/((200+t)^2)+(200+t))/(200+t)\right)`

`= \lim\limits_(t \to \infty) \left((4\cdot 10^6)/((200+t)^3)+1\right)`

`=1`

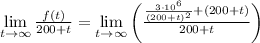
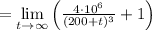
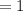
Hence, the theoretical limiting concentration of an infinite tank is
`1` lb per gallon.