Question

Let n>=1.

Prove by induction for all
n>=1 1+5+9+...+[4(n-1)+1]+[4n+1] = (n+1)(2n+1).

Answer 1

Proved

Explanation:

Given

`1+5+9+...+[4(n-1)+1]+[4n+1] = (n+1)(2n+1)`

`n \geq 1`

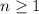
Required

Prove by induction

`1+5+9+...+[4(n-1)+1]+[4n+1] = (n+1)(2n+1)`

Increment n by 1 on both sides

`1+5+9+...+[4(n-1)+1]+[4n+1]+[4(n+1)+1] = (n+1+1)(2(n+1)+1)`

Simplify the right hand side

`1+5+9+...+[4(n-1)+1]+[4n+1]+[4(n+1)+1] = (n+2)(2n+2+1)`

`1+5+9+...+[4(n-1)+1]+[4n+1]+[4(n+1)+1] = (n+2)(2n+3)`

Group the left hand side

`(1+5+9+...+[4(n-1)+1]+[4n+1])+[4(n+1)+1] = (n+2)(2n+3)`

Recall that

`1+5+9+...+[4(n-1)+1]+[4n+1] = (n+1)(2n+1)` ----[Given]

So; Substitute
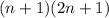`(n+1)(2n+1)` for
`1+5+9+...+[4(n-1)+1]+[4n+1]` on the left hand side

`(n+1)(2n+1)+[4(n+1)+1] = (n+2)(2n+3)`

Open All Brackets

`2n^2 + n + 2n + 1 + 4n + 4 + 1 = 2n^2 + 3n + 4n + 6`

Collect Like Terms

`2n^2 + n + 2n + 4n+ 1 + 4 + 1 = 2n^2 + 3n + 4n + 6`

`2n^2 + 7n+ 6 = 2n^2 + 7n + 6`

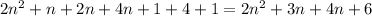
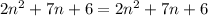
Notice that the expression on both sides are equal;

Hence, the given expression has been proven