Question

The wavelength of green light is 550 nm.

Required:
a. If an electron has the same wavelength, determine the electron velocity and momentum.
b. Repeat part (a) for red light with a wavelength of 440 nm.
c. For parts (a) and (b), is the momentum of the photon equal to the momentum of the electron?

Answer 1

(a) momentum of photon is 1.205 x 10⁻²⁷ kgm/s

velocity of electron is 1323.88 m/s

momentum of the electron is 1.205 x 10⁻²⁷ kgm/s

(b) momentum of photon is 1.506 x 10⁻²⁷ kgm/s

velocity of electron is 1654.85 m/s

momentum of the electron is 1.506 x 10⁻²⁷ kgm/s

(c) The momentum of the photon is equal to the momentum of the electron

Step-by-step explanation:

(a)

wavelength of green light, λ = 550 nm

momentum of photon is given by;

`p = (h)/(\lambda)\\\\ p = (6.626 *10^(-34))/(550*10^(-9))\\\\p = 1.205 *10^(-27) \ kg.m/s`

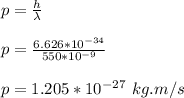
velocity of electron is given by;

`P = (h)/(\lambda) \\\\mv = (h)/(\lambda)\\\\v = (h)/(m \lambda)\\\\v = (6.626 *10^(-34))/((9.1*10^(-31) )(550*10^(-9)))\\\\v = 1323.88 \ m/s`

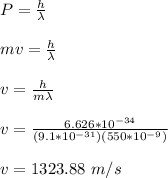
momentum of the electron is given by;

p = mv

p = (9.1 x 10⁻³¹) (1323.88)

p = 1.205 x 10⁻²⁷ kgm/s

(b)

wavelength of red light, λ = 440 nm

momentum of photon is given by;

`p = (h)/(\lambda)\\\\ p = (6.626 *10^(-34))/(440*10^(-9))\\\\p = 1.506 *10^(-27) \ kg.m/s`

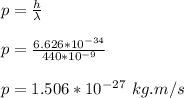
velocity of electron is given by;

`v = (6.626 *10^(-34))/((9.1*10^(-31) )(440*10^(-9)))\\\\v = 1654.85 \ m/s`

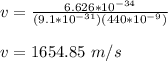
momentum of the electron is given by;

p = mv

p = (9.1 x 10⁻³¹) (1654.85)

p = 1.506 x 10⁻²⁷ kgm/s

(c) The momentum of the photon is equal to the momentum of the electron.