Question

A rocket moves straight upward, starting from rest with an acceleration of +29.4 m/s2 . It runs out of fuel at the end of 4.00s and continues to coast upward, reaching a maximum height before falling back to earth. (a) Find the rocket’s velocity and position at the end of 4.00s. (b) Find the maximum

Answer 1

a) The velocity and position of the rocket at the end of 4 seconds are 117.6 meters per second and 235.2 meters, respectively, b) The maximum height reached by the rocket is 940.296 meters, c) The rocket crashes on the ground at a velocity of -96.030 meters per second.

Step-by-step explanation:

The complete statement is:

A rocket moves straight upward , starting from rest with an acceleration of 29.4 m/s2. it runs out of fuel at the end of 4.00 s and countinues to coast upward , reaching a maximum height before falling back to earth . a) find the rocket's velocity and position at the end of 4.00 s . b) Find the maximum height the rocket reaches. c) find the velocity on the instant before the rocket crashes on the ground.

a) The rocket accelerates uniformly, whose equations of motion are:

`y = y_(o) + v_(o)\cdot t + (1)/(2)\cdot a \cdot t^(2)`

`v = v_(o) + a\cdot t`

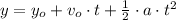
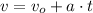
Where:

`y` - Final position, measured in meters.

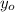`y_(o)` - Initial position, measured in meters.

`v_(o)` - Initial velocity, measured in meters per second.

`t` - Time, measured in second.

`a` - Acceleration, measured in meters per square second.

`v` - Final velocity, measured in meters per second.

If we know that
`y_(o) = 0\,m`,
`v_(o) = 0\,(m)/(s)`,
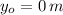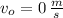`t = 4\,s` and
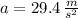`a = 29.4\,(m)/(s^(2))`, the velocity and position of the rocket are, respectively:

`y = 0\,m+\left(0\,(m)/(s) \right)\cdot (4\,s)+(1)/(2)\cdot \left(29.4\,(m)/(s^(2)) \right) \cdot (4\,s)^(2)`

`y = 235.2\,m`

`v = 0\,(m)/(s) + \left(29.4\,(m)/(s^(2))\right)\cdot (4\,s)`

`v = 117.6\,(m)/(s)`

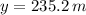
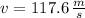
The velocity and position of the rocket at the end of 4 seconds are 117.6 meters per second and 235.2 meters, respectively.

b) Now, the rocket experiments a free-fall motion. The maximum height of the rocket is obtained by equalizing the equation of velocity to zero and evaluating the equation of position later. That is:

`y = 235.2\,m+\left(117.6\,(m)/(s) \right)\cdot t+(1)/(2)\cdot \left(-9.807\,(m)/(s^(2)) \right) \cdot t^(2)`

`v = 117.6\,(m)/(s)+\left(-9.807\,(m)/(s^(2)) \right)\cdot t`

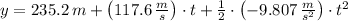
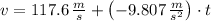
Then,

`0 = 117.6 -9.807\cdot t`

`t = 11.991\,s`

The maximum height reached by the rocket is:

`y = 235.2+117.6\cdot (11.991)+(1)/(2)\cdot (-9.807)\cdot (11.991)^(2)`

`y = 940.296\,m`

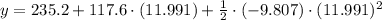
The maximum height reached by the rocket is 940.296 meters.

c) The rocket experiments a free-fall motion and is accelerated by gravity until collision happens. The equations of motion below are presented:

`0\,m = 940.296\,m+\left(0\,(m)/(s) \right)\cdot t+(1)/(2)\cdot \left(-9.807\,(m)/(s^(2)) \right) \cdot t^(2)`

`v = 0\,(m)/(s)+\left(-9.807\,(m)/(s^(2)) \right)\cdot t`

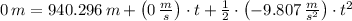
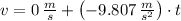
From the equation of position we get the instant when rocket hits the ground, whose roots are found by Quadratic Formula:

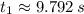`t_(1) \approx 9.792\,s` and
`t_(2) \approx -9.792\,s`

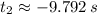
Only the first root is physically reasonable.

By the second equation we calculate the final velocity:

`v = 0-9.807\cdot (9.792)`

`v = -96.030\,(m)/(s)`

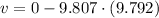
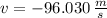
The rocket crashes on the ground at a velocity of -96.030 meters per second.