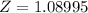Answer:
a
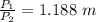
b
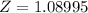
Step-by-step explanation:
From the question we are told that
The filament temperature of the first bulb is
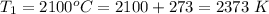
The filament temperature of the second bulb is
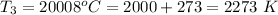
Generally according to Stefan-Boltzmann law the power emitted by first bulb is mathematically represented as
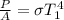
Here
 is the Stefan-Boltzmann with value
is the Stefan-Boltzmann with value
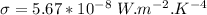
So
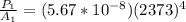
=>
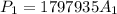
Generally according to Stefan-Boltzmann law the power emitted by second bulb is mathematically represented as
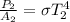
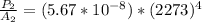
=>
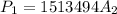
Given that the two bulbs are identical we have that
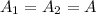
So
The ration is mathematically represented as
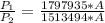
=>
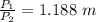
Generally the area is mathematically represented as
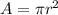
Recall that
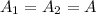
=>
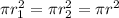
=>
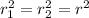
Now if the radius of the cooler bulb is increase by a factor Z (i.e Z * r )then the area of the cooler bulb
![A_2 [\tex] becomes </p><p> [tex] A_2 = (Zr)^2](https://img.qammunity.org/2021/formulas/physics/college/owvxl8d14z1c95hzgtu3m3mhwl6mj10g24.png)
=>
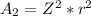
Here Z is the factor by which it is made thicker
So For
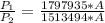
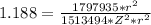
=>