Answer:
d. (0.5457 , 0.8361)
Explanation:
From the missing findings recorded in the Excel output; we have:
the sample size to be = 55
count of response = 38
So, the proportion of parents that have the feeling they do spend little time with their children are :
p =
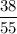
p= 0.69
Thus, p = sample mean
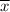 = 0.69
= 0.69
The standard error of the proportion p is expressed as:
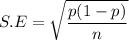
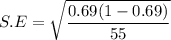

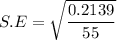
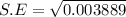
S.E = 0.06236
At 98% confidence interval level, the level of significance = 1 - 0.98 = 0.02
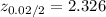
Confidence interval =
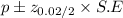
Confidence interval =
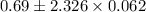
Confidence interval =
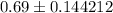
Confidence interval =
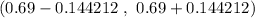
Confidence interval =
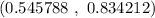
Thus, option d. (0.5457 , 0.8361) is the right answer