Question

the sum of the angle measures of any triangle is 180 degrees. Find the angle measures of a triangle if the second angle is 10 degrees less than twice the fist, and the third angle measures 25 degrees more than the second

Answer 1

Angle 1 is 35°, angle 2 is 60°, and angle 3 is 85°

Explanation:

In seeing the measures of the angles from the problem, we see that angle 1 can be represented as x, and all the other angles rely on the value of x, so then an equasion can be built.

Angle 1 is represented as x,

Since angle 2 is 10 less than 2 times angle 1's value, it is represented as 2x-10.

Since angle 3 is 25 more than the second, you add 25 to angle 2's value, which leaves us with 2x+15.

In adding all these values together, we get
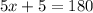`5x+5=180`. We then subtract 5 from both sides, leaving us with
`5x=175`, and then we divide both sides by 5 to get
`x=35`.

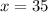We then plug in x's value to find the measures of the angles.

For angle 1:35=35,

For angle 2: 2(35)-10=60

For angle 3: 2(35)+15=85.

Finally, to double check, add the values of 35, 60, and 85 together, which equals 180