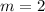Answer:
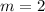
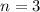
Explanation:
Given
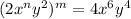
Required
Solve for m and n
Start by opening the bracket using laws of indices
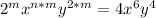
Express 4 as 2²
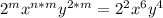
Compare both sides of the equation, we have:
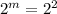 --- (1)
--- (1)
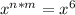 --- (1)
--- (1)
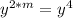 ---- (2)
---- (2)
In (1)
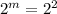
2 cancels out on both sides; so, we have
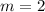
In (2)
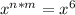
x cancels out on both sides; so, we have

Substitute 2 for m
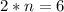
Divide through 2
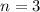
In (3)
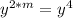
y cancels out on both sides; so, we have
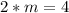
Divide through 2