Question

An investigator compares the durability of two different compounds used in the manufacture of a certain automobile brake lining. A sample of 71 brakes using Compound 1 yields an average brake life of 41,628 miles. A sample of 31 brakes using Compound 2 yields an average brake life of 36,379 miles. Assume the standard deviation of brake life is known to be 4934 miles for brakes made with Compound 1 and 4180 miles for brakes made with Compound 2. Determine the 98% confidence interval for the true difference between average lifetimes for brakes using Compound 1 and brakes using Compound 2. Step 1 of 2 : Find the critical value that should be used in constructing the confidence interval.

Answer 1

98% Confidencce Interval is ( 3030.6, 7467.4 )

Explanation:

Given that:

Sample size
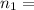`n_1 =` 71

Sample size
`n_2 =` 31

Sample mean
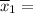`\overline x_1 =` 41628

Sample mean
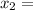`x_2 =` 36,379

Population standard deviation
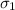`\sigma_1` = 4934

Population standard deviation
`\sigma_2 =` 4180

At 98% confidence interval level, the level of significcance = 1 - 0.98 = 0.02

Critical value at
`z_(0.02/2) = 2.33`

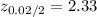
The Margin of Error =
`z * \sqrt{(\sigma_1^2)/(n_1)+(\sigma^2_2)/(n_2) }`

=
`2.33 * \sqrt{(4934^2)/(71)+(4180^2)/(31) }`

=
`2.33 * \sqrt{(24344356)/(71)+(17472400)/(31) }`

=
`2.33 * √(906504.06 )`

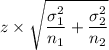
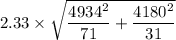
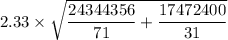
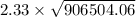
= 2218.40

The Lower limit =
`( \overline x_1 - \overline x_2) - (Margin \ of \ error)`

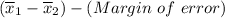
= ( 41628 - 36379 ) - ( 2218.40)

= 5249 - 2218.40

= 3030.6

The upper limit =
`( \overline x_1 - \overline x_2) + (Margin \ of \ error)`

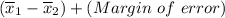
= ( 41628 - 36379 ) + ( 2218.40)

= 5249 + 2218.40

= 7467.4

∴ 98% Confidencce Interval is ( 3030.6, 7467.4 )