Answer :
98°
Step by step Step-by-step explanation :
As we can see in figure,
∠F = 53°
∠H = 45°
So,
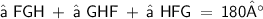
[Angle sum property, which states that the sum of all the angles of a triangle is 180°]
=> ∠FGH + 45° + 53° = 180°
=> ∠FGH = 180° - 98°
=>
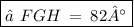
Now,
∠x + ∠FGH = 180°
[linear pair]
=> ∠x = 180° - 82°
=>
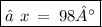
Alternative Method :
We know that sum of two opposite interior angles is equal to the exterior angle.
So
∠x = ∠GHF + ∠HFG.
=> ∠x = 45 ° + 53°
=>
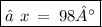
Hope this helps!