Question

Endpoints of segment MN have coordinates (0, 0), (5, 1). The endpoints of segment AB have coordinates (1 1/22 , 2 1/4 ) and (−2 1/4 , k). What value of k makes these segments perpendicular?

Answer 1

Answer:
`k=18(8)/(11)`.

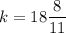Explanation:

If a line passing through two points, then

`Slope=(y_2-y_1)/(x_2-x_1)`

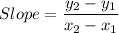
Endpoints of segment MN have coordinates (0, 0) and (5, 1).

Slope of MN
`=(1-0)/(5-0)=(1)/(5)`

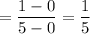
The endpoints of segment AB have coordinates
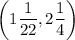`\left(1(1)/(22) , 2(1)/(4)\right)` and
`\left(-2(1)/(4) , k\right)`.

`A=\left(1(1)/(22) , 2(1)/(4)\right)=\left((23)/(22) ,(9)/(4)\right)`

`B=\left(-2(1)/(4) , k\right)=\left(-(9)/(4) , k\right)`.

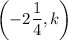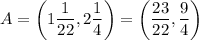
Slope of AB
`=(k-(9)/(4))/(-(9)/(4)-(23)/(22))`

`=((4k-9)/(4))/((-99-46)/(44))`

`=(4k-9)/(4)* (44)/(-145)`

`=4k-9* (11)/(-145)`

`=(44k-99)/(-145)`

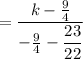
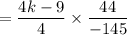
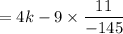
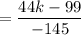
Product of slopes of two perpendicular segments is -1.

Slope of MN × Slope of AB = -1

`(1)/(5)* (44k-99)/(-145)=-1`

`(44k-99)/(-725)=-1`

`44k-99=725`

`44k=725+99`

`k=(824)/(44)`

`k=(206)/(11)`

`k=18(8)/(11)`

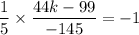
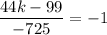
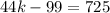
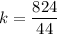
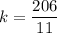
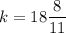
Therefore, the value of k is
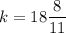`k=18(8)/(11)`.

Answer 2

k=21

Explanation:

Find the slope of MN which is 1/5, (use the slope formula.)

Use the slope formula for AB using k as y_2

Substitute and you get k=21

21-2.25/-2.25-1.5=-5

The lines are perpendicular because the slopes are the negative reciprocal of one another.