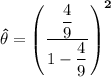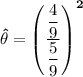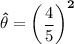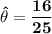Question

Let X1,..., Xn be a simple random sample from a distribution with density function Svorvo-1 O<331 fx (2:0) = otherwise where e > 0 is an unknown parameter.

(a) Find a MOM estimator for 0.
(b) If the observations are 1 1 1 2'3'2 Determine the point estimate with the estimator you find in part (a).

Answer 1

The method of moment (MOM) estimator as:
`\mathbf{\hat {\theta} =((\overline X)/(1-\overline X))^2}`

`\overline X = (4)/(9)`

`\mathbf{\hat {\theta} =(16)/(25) }`

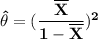
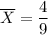
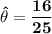
Explanation:

From the question, the correct format for the probability density function is:

`fx(x ; \theta) = \left \{ {{√(\theta x)^(√(\theta)-1)}\ \ 0 \leq x \leq 1 \atop {0} \ \ \ \ \ \ \ otherwise } \right.`

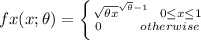
where θ > 0 is an unknown parameter.

(a) The MOM estimator can be calculated as follows:

`E(X) = \int ^1_0x. √(\theta) \ x^(√(\theta)-1) \ dx`

`E(X) = \int ^1_0 √(\theta) \ x^(√(\theta)) \ dx`

`E(X) = (√(\theta) )/(√(\theta) +1 ) ( x ^(√(\theta)+1))^1_0`

`E(X) = (√(\theta) )/(√(\theta) +1 )`

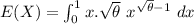
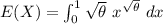
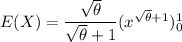
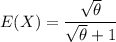
suppose E(X) =
`\overline X`

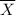
Then;

`\overline X = (√(\theta) )/(√(\theta) +1 )`

`(1)/(\overline X) = (√(\theta) +1 )/(√(\theta))`

`(1)/(\overline X) =1 + (1)/(√(\theta))`

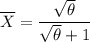
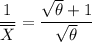
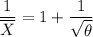
making
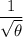`(1)/(√(\theta))` the subject of the formula, we have:

`(1)/(√(\theta)) =(1)/(\overline X) - 1`

`(1)/(√(\theta)) =(1-\overline X)/(\overline X)`

`√(\theta) =(\overline X)/(1-\overline X)`

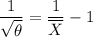
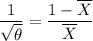
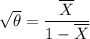
squaring both sides, we have:

The method of moment (MOM) estimator as:
`\mathbf{\hat {\theta} =((\overline X)/(1-\overline X))^2}`

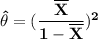
b) If the observations are
`(1)/(2), (1)/(3), (1)/(2)`

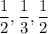
Then,

`\overline X = ((1)/(2)+ (1)/(3)+(1)/(2))/(3)`

`\overline X = ((3+2+3)/(6))/(3)`

`\overline X = ((8)/(6))/(3)`

`\overline X = (8)/(6) * (1)/(3)`

`\overline X = (8)/(18)`

`\overline X = (4)/(9)`

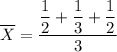
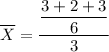
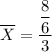
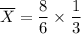
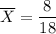
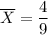
Finally, the point estimate of the estimator
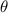`\theta` is

`\mathbf{\hat {\theta} =\begin {pmatrix} ((4)/(9))/(1-(4)/(9)) \end {pmatrix}^2}`

`\mathbf{\hat {\theta} =\begin {pmatrix} ((4)/(9))/((5)/(9)) \end {pmatrix}^2}`

`\mathbf{\hat {\theta} =\begin {pmatrix} (4)/(5) \end {pmatrix}^2}`

`\mathbf{\hat {\theta} =(16)/(25) }`